Como sabemos, en Houdini podemos realizar una misma tarea de muchas formas: algunas óptimas y otras no tan eficientes. Por lo tanto, siempre, como rule of thumb, lo que nos indicará el camino es tratar de optimizar el procesamiento y mantenerlo eficiente.

Quiero plantear dos formas de hacer esto: una versión rápida, para quienes no quieran adentrarse tanto en el tema, y otra versión más profunda, donde exploraremos las similitudes con otros procesos.

video

Usando VEX y Wrangles

Bien, arrancamos por la versión extendida.

Pero… ¿por qué extendida? Seguro estás pensando: ¿Es más compleja, con código y todo eso?

¿Cuál sería el objetivo? Bueno, lo complicamos con un solo propósito: tratar de mantener el control total sobre lo que sucede a lo largo de toda la cadena. Y esto nos da una gran ventaja: en cualquier momento, durante la construcción de nuestro sistema, podemos modificarlo y personalizarlo para crear efectos derivados.

O sea, en síntesis, tenemos mayor control sobre el resultado final, aunque la complejidad es más alta, lo cual mueve la aguja de equilibrio que nos marca nuestra máxima de óptimo y simple. Quizás para algún efecto que no sea principal esto resulte demasiado, pero para comportamientos más complejos y personalizados necesitamos tener este nivel de control.

Sin embargo, podemos encontrar niveles intermedios gracias a la gran cualidad modular o nodal de Houdini.

Estuve probando toda esta semana algunos caminos posibles y me topé con varias alternativas que están muy interesantes. Siempre quiero recalcar que toda la información provista en este blog debe ser puesta en duda y llevada a la práctica: así aprenderemos todos.

Create particles

// create particles
int num = chi("num"); // number of particles, set to 1500
float speed;

for (int i = 0; i < num; i++) {
    vector Pos = set(rand(i + chf("seed")), 0.0, rand(i));
    vector orient = 0;
    speed = fit01(rand(i), 0.5, 1.0);
    // init Particles
    int pt = addpoint(0, Pos);
    setpointattrib(0, "dir", pt, orient);
    setpointattrib(0, "speed", pt, speed);
}

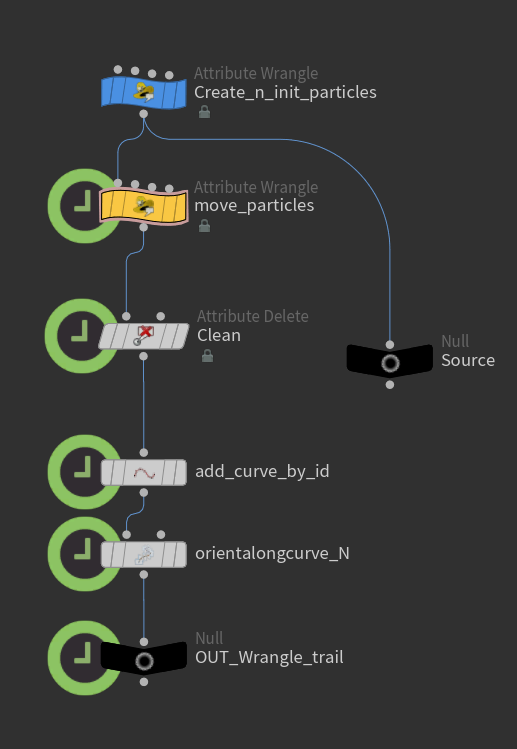
En el primer Wrangle vamos a crear nuestras partículas y asignarles una ubicación al azar entre 0 y 1. Después de esto, a cada punto le vamos a dar una orientación aleatoria y una velocidad (speed) también aleatoria, que va desde 0.5 hasta 1.

Bien, después vamos a iterar independientemente sobre cada punto para dibujar su movimiento según su velocidad y el campo vectorial generado por el ruido.

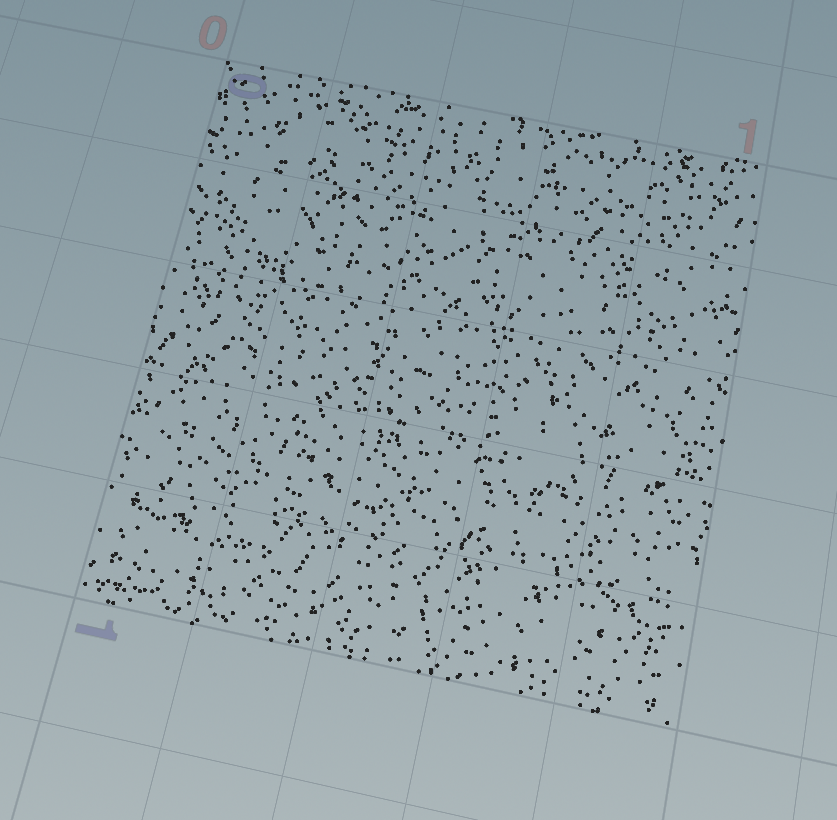
Create trails (move_particles)

// Create trails (move_particles)

// set global variables
float noiseScale = chf("Noise_Scale");
float noiseStrength = chf("Noise_Strength");
int trail = chi("Trail");
float TWO_PI = 2.0 * M_PI;

@id = @ptnum;
@Cd = 0;

removepoint(0, @ptnum);

// Move particles
for (int i = 0; i < trail; i++) {
    vector pos = @P;
    vector angle = noise((@P + chf("offset_x")) / noiseScale) * TWO_PI * noiseStrength;
    vector dir = set(cos(angle.x), 0, sin(angle.y));
    vector vel = dir * (@speed * chf("mult_vel"));
    removepoint(0, @ptnum);
    int pt = addpoint(0, @P);
    @P += vel;
    setpointattrib(0, "id", pt, @id);
    setpointattrib(0, "Cd", pt, angle);
}

Esta parte nos puede recordar un poco a nuestro código en p5.js. En VEX es posible crear funciones personalizadas para procesar geometría, muy parecido a lo que hacíamos con las clases en Processing.

Pero esta vez vamos a continuar de la manera más tradicional, para mantenerlo simple y eficiente.

Usamos exactamente la misma sintaxis que empleamos para definir el loop for. En realidad, es lo mismo, pero en el caso anterior usábamos un for dentro de otro for. Bueno, en este caso, al asignar un Wrangle en modo Points, lo que ocurre es que Houdini ejecuta todo este código una vez por cada punto. Entonces, el resultado sería el mismo: un for dentro de otro for.

Línea a línea

Vamos paso por paso y veamos qué hacemos en cada punto:

for (int i = 0; i < trail; i++) {
    {...}
}

Lo que estamos diciendo acá es que, por cada punto, vamos a hacer un bucle (loop) el número de veces que se indique en la variable trail. Si, por ejemplo, tenemos un valor de 7 y contamos con 1500 partículas, eso significa que vamos a iterar 7 veces por cada punto, lo que nos daría un total de 7 × 1500 = 10.500 iteraciones. Bien, sigamos.

for (int i = 0; i < trail; i++) {
    vector pos = @P;
    vector angle = noise((pos + chf("offset_x")) / noiseScale) * TWO_PI * noiseStrength;
    vector dir = set(cos(angle.x), 0, sin(angle.y));
    vector vel = dir * (@speed * chf("mult_vel"));
    {...}
}

Vector pos = @P;

En la variable pos, que es un vector, vamos a guardar la posición actual de nuestra partícula. Si es la primera iteración, vamos a guardar la posición aleatoria que generamos previamente. Y si desplazamos la partícula en la siguiente iteración, vamos a sobrescribir esa información con la nueva posición.

Usualmente, esto se hace para mantener el código más limpio y explícito, a menos que queramos usar esa versión anterior de la posición con algún otro fin.

Vector angle

Este pedazo de código es exactamente igual a lo que haríamos en p5.js y, en realidad, está haciendo lo mismo. La función noise nos devuelve valores entre 0 y 1, y los multiplicamos por TWO_PI para convertirlos a 360 grados, junto con un modificador (noiseStrength) para ampliar o escalar esos valores.

Vector dir

De cada valor obtenido, sampleamos las funciones cos y sin para obtener un ángulo según el valor muestreado, más su modificación (noiseStrength).

Vector vel

Bien, acá vamos a mover la partícula en la orientación que obtuvimos en dir. Mientras más alto sea el valor de speed, más se va a desplazar. Como extra, agregamos un multiplicador (en este caso, mult_vel) que nos va a ayudar a controlar la magnitud, para decidir si el movimiento es más intenso o más suave.

for (int i = 0; i < trail; i++) {
    {...}
    int pt = addpoint(0, pos);
    @P += vel;
    setpointattrib(0, "id", pt, @id);
    setpointattrib(0, "Cd", pt, angle);
}

int pt

En cada iteración, creamos un punto en la posición original o en la posición anterior.

@P += vel;

A esa posición le sumamos el desplazamiento en la dirección que definimos, multiplicado por speed, que determina cuánto se va a mover desde su punto de inicio.

La siguiente línea es utilitaria y no necesariamente obligatoria:

set id

Copiamos el id del punto de partida a lo largo de toda la cadena, para después poder conectarlos mediante un nodo Add.

Y así obtenemos un resultado muy, muy parecido a lo que logramos en Processing o en la versión más corta.

Posteriormente, agrego un nodo Add para conectar todos los puntos que tienen el mismo id, y un Orient Along Curve para calcular la dirección de la tangente y guardarla como N.

Bueno, en este caso no quise quedarme ahí y decidí llevarlo a otro nivel más complejo. Lo voy a tratar de explicar un poco más rápido, porque involucra técnicas extra, pero en esencia, el concepto sigue siendo el mismo, solo que ahora dentro de DOPs.

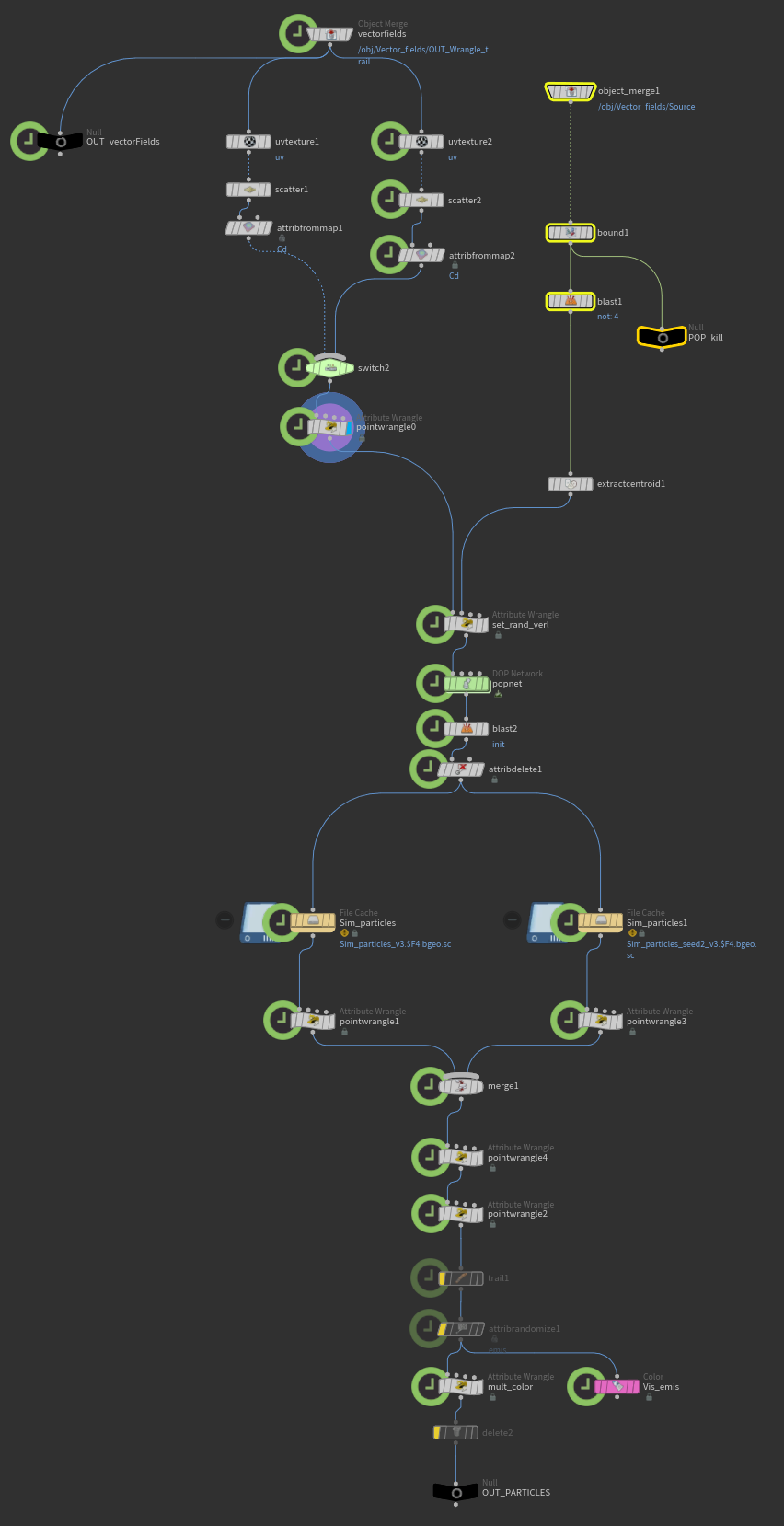
Dentro de un Solver, con un Geometry VOP usando Point Clouds, voy a samplear (muestrear) la dirección según la posición actual de mi partícula y la voy a copiar, manteniendo su velocidad actual.

O sea, si mi partícula tiene una magnitud de 3 y una dirección de (0, 1, 0.5), entonces, dentro del Geometry VOP, lo que hago es tomar su posición en el espacio, samplearla contra el vector trail que creamos, y copiar solo la dirección. Después, multiplico esa dirección por la magnitud original (3) que ya tenía la partícula.

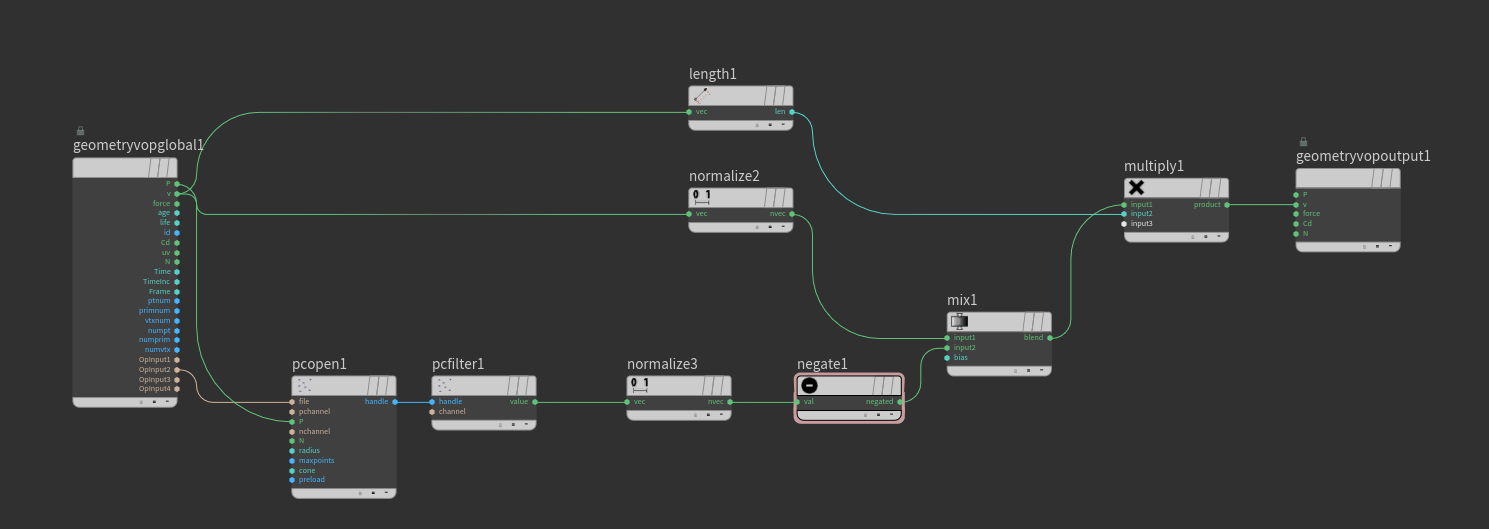
Así mantengo su velocidad actual, pero cambio solo la orientación. Eso sí, hay que aclarar que debemos normalizar el ángulo (vector) que sampleamos del vector trail original para asegurarnos de que esté correcto.

El resultado es más que interesante.

Usando Volume Trail

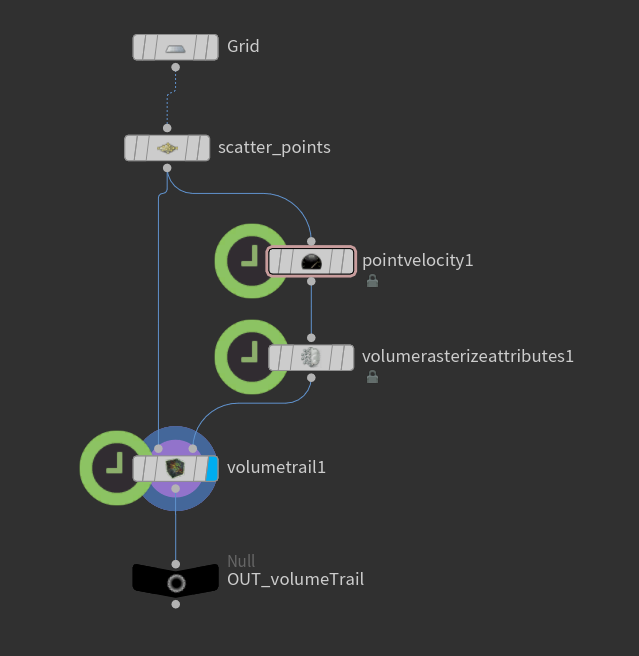
Primero, vamos a crear nuestras partículas dispersas dentro de un contenedor, que en este caso es un plano.

Ahora necesitamos un volumen que dibuje nuestros trails. Aquí podemos generarlos como queramos, pero lo que voy a hacer es crear un Perlin Noise y agregarlo como velocidad a cada punto. Después, voy a rasterizar esta información en un Velocity Volume usando un nodo de rasterización de partículas llamado Volume Rasterize Attributes, que toma cada una de nuestras partículas y las convierte en el volumen que necesitamos.

En este caso, será un volumen vectorial, porque nuestra velocidad es un vector que tiene magnitud y dirección, perfecto para desplazar y dibujar nuestros trails.

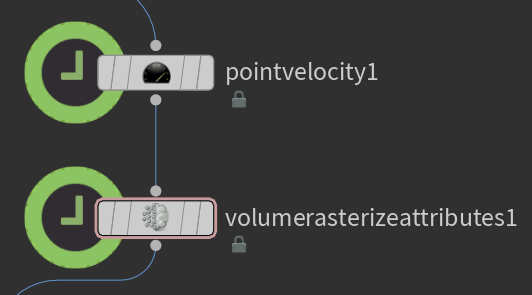
Como mencionamos, nuestro nodo Volume Trail exige dos inputs: Points to Trail y Velocity Volumes.

Conectamos nuestros inputs y ¡pum! Nuestros trails son desplazados por la velocidad de nuestros volúmenes.

Posteriormente, podemos renderizarlos como strands y obtener hermosos resultados.

Bien, hemos llegado lejos, y sé que puede ser difícil entender todo esto de una sola vez, pero creo que son técnicas muy valiosas para darle un valor agregado a nuestras creaciones, ya sea en Houdini o en cualquier otro programa que nos permita aplicar una lógica similar.

Con esto concluimos la Parte 2 de nuestra serie, y es momento de hacer algo más tangible.

En el siguiente post, vamos a recrear exactamente lo mismo usando un Raspberry Pi y MicroPython.

Si llegaron hasta acá, ¡abrazos! Y nos vemos en el próximo post.